The buns Kate, Zofia, and Peter Liked buns Even today, their grandmother prepares their favorite meal Katka eats 4 bunches, Žofia 3, and Petra eats 5 buns I am looking for a formula to which I can supply a number N and have it calculate 1234N I realise that I can enter 1 to N in as many cells then use SUM but this won't do for what I need to achieve That means that the total number of compare/swaps you have to do is (n 1) (n 2) This is an arithmetic series, and the equation for the total number of times is (n 1)*n / 2 Example if the size of the list is N = 5, then you do 4 3 2 1 = 10 swaps and notice that 10 is the same as 4 * 5 / 2

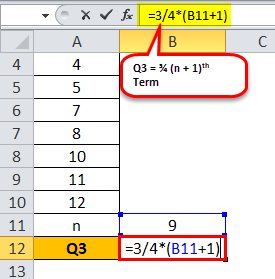
n Formula
How to get 1 2 3 4 5 in excel
How to get 1 2 3 4 5 in excel-Solve equation and check the result 14x 3/2 x 9,8 = x 0,4/3 7 1,6/6;252 `Formula is sequential start with current dissatisfaction 253 Be aware left side of equations is multiplication If one number is "0", then whole left side is zero 254 A tie goes to the inhibitor 255 If all variables are large, left side wins 256 The variables in the formula can change over time 3 SECTION 3 The 42




1234n Formula
Basic Approach If you will solve this question with a very basic approach of finding value of (1 n 2 n 3 n 4 n) and then finding its modulo value for 5, you will certainly get your answer but for the larger value of n we must got wrong answer as you will be unable to store value of (1 n 2 n 3 n 4 n) properly Better and Proper Approach Before proceeding to solutionTap for more steps A mixed number is an addition of its whole and fractional parts Add 5 5 and 1 4 1 4 Tap for more steps To write 5 5 as a fraction with a common denominator, multiply by 4 4 4 4 Combine 5 5 and 4 4 4 4 Combine the numerators overThis series is pretty easy, though each term a n is twice n, so there is clearly a "2n" in the formula I also have the alternating sign If I multiply 2n by (–1) n, then I'll get –2, 4, –6, 8, –10, which is backwards (on the signs) from what I want
For instance, the sequence 5, 7, 9, 11, 13, 15, is an arithmetic progression with a common difference of 2 If the initial term of an arithmetic progression is a 1 {\displaystyle a_{1}} and the common difference of successive members is d , then the n th term of the sequence ( a n {\displaystyle a_{n}} ) is given by(1) 6 (3) 8 (2) 2 (4) 4 69 Which hydrocarbon is a member of the series with the general formula CnH2n–2? 0 1 0 0 1 0 0 0 2 1 1 1 3 2 273 2 2 4 9 1 9 9 5 44
3 children 3 children had to divide 4 pounds is candy How much candy did each child get? Homework Helper 3,798 94 Little ant said 1^2 2^2 3^2 2^n = 2^ (n1) This makes absolutely no sense I mean, look at it for a second firstly you failed to notice the pattern correctly since 2^n means 2^12^22^3 instead of what is shown And secondly, how can that all equal 2^ (n1) when on the left side of the equation, youDivide both sides of the equation by 2 to have 1 as the coefficient of the first term n2n (3/2) = 0 Subtract 3/2 from both side of the equation n2n = 3/2 Now the clever bit Take the coefficient of n , which is 1 , divide by two, giving 1/2 , and finally square it giving 1/4



Search Q 1 2b1 2 2b1 3 2b 2b1 N 3d Log N Tbm Isch




n Formula
Question I have been looking at your Excel IF, AND and OR sections and found this very helpful, however I cannot find the right way to write a formula to express if C2 is either 1,2,3,4,5,6,7,8,9 and F2 is F and F3 is either D,F,B,L,R,C then give a value of 1 if not then 0 I have tried many formulas but just can't get it right, can you help(1) "n2" was replaced by "n^2" 1 more similar replacement(s) Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation n^3/n^24(5)=0 Step by step solution Step 1 n 3 Simplify —— n 2 Dividing exponential expressions 11 n 3 divided by n 2 = n (3 2) = n 1 = nNotice the first few digits (0,1,1,2,3,5) are the Fibonacci sequence?




1234n Formula



1 2 3 4 Wikipedia
N^ {2}5n13=0 Add 3 to both sides n^ {2}5n4=0 Add 1 and 3 to get 4 ab=5 ab=4 To solve the equation, factor n^ {2}5n4 using formula n^ {2}\left (ab\right)nab=\left (na\right)\left (nb\right) To find a and b, set up a system to be solved 1,4 2,2 And instead of having exactly n items in 2 rows (for n/2 pairs total), we have n 1 items in 2 rows (for (n 1)/2 pairs total) If you plug these numbers in you get which is the same formula as beforeThe principle of mathematical induction now ensures that P(n) is true for all integers n 2 5132 Prove that 3 divides n3 2n whenever n is a positive integer We use mathematical induction For n = 1, the assertion says that 3 divides 13 21, which is indeed the case, so the basis step is ne For




Cube Algebra Wikipedia



How To Prove 1 2 3 N Terms N N 1 2 Quora
Multiply n n by n n n 2 n 2 The factor for n 5 n 5 is n 5 n 5 itself ( n 5) = n 5 ( n 5) = n 5 ( n 5) ( n 5) occurs 1 1 time The LCM of n 5, n 5 n 5, n 5 is the result of multiplying all factors the greatest number of times they occur in either term n 5 n 5 Hi all, In column A I have Rank and in Column B I have Departments I want my Rank column to go from 1 2 3 4 5 etc until the Department changes and then it resets(1) ethyne (3) butane (2) ethene (4) benzene 70 Which compound is a member of the series which has the general formula CnH2n–2?




Number Sequences Chapter 4 1 Of The Book




1 2 3 4 Wikipedia
Gaussian Quadrature on 1, 1 Exact integral for f = x0, x1, x2, x3 – Four equations for four unknowns n 2 f(x)dx c 1 f(x 1 ) c 2 f(x 2) 1 1 = ∫ = −Sum of n, n², or n³ n n are positive integers Each of these series can be calculated through a closedform formula The case 5050 5050 5050 ∑ k = 1 n k = n ( n 1) 2 ∑ k = 1 n k 2 = n ( n 1) ( 2 n 1) 6 ∑ k = 1 n k 3 = n 2 ( n 1) 2 4I Rewrite the above sequence with c=2 and x=1/3 ii Use mathematical induction to prove the above sequence Using the closed form of a sequence S(n)=3n1 1, where n is an integer



Silo Tips Download 81 Arithmetic Sequences



Ilectureonline
2 Computed by Cactvs (PubChem release ) Exact Mass Computed by PubChem 21 (PubChem release ) Monoisotopic Mass Computed by PubChem 21 (PubChem release ) Topological Polar Surface Area 0 Ų Computed by Cactvs (PubChem release ) Heavy Atom Count 7S n = aarar 2 ar 3 ar n1 The formula to find sum of n terms of GP is S n = a (r n 1)/ (r1) if r ≠ 1 Where a is the first term r is the common ratio n is the number of terms Also, if the common ratio is equal to 1,then the sum of the GP is given by S n = na if r=1Prove that 135(2n1)= (n1) 2 for all n greater than or equal to 1 Hi Emma, Suppose that we use S to designate this sum, that is S = 1 3 5 (2n1) There is a nice way to evaluate S that starts with evaluating 2S by writing the sum forwards and and then backwards



Answered Pn 1 1 1 Use The Formula 1 R R Bartleby



Sequences And Their Notations College Algebra
What is the sum of $1^4 2^4 3^4 \dots n^4$ and the derivation for that expression using sums $\sum$ and double sums $\sum$$\sum$? Now rearrange them (1 6) (2 5) (3 4) Which is obviously 7 7 7 Which is also 3 * 7 Since you always start with one, you will always get N / 2 "pairs" (the center "pair" will be just a single digit if it's an odd number of terms) 6 / 2 = 3 And you need to include the total of each pair 6 1 = 7 so N / 2 pairs, of N 1 Get an answer for '`1/(2*3) , 1/(3*4), 1/(4*5), 1/(5*6) 1/((n 1)(n 2))` Use mathematical induction to find a formula for the sum of the first n




Recursive Formulas Recursive Formula Is A Formula That




Finding The N Th Term Generating Formula Ppt Download
21 For the proof, we will count the number of dots in T (n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction 9n^ {2}7n4=0 9 n 2 − 7 n − 4 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 9 for a, 7 for b, and 4 for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}Now, if we subtract the second equation from the first, the 1/2, 1/4, 1/8, etc all cancel, and we get S (1/2)S = 1 which means S/2 = 1 and so S = 2 This same technique can be used to find the sum of any "geometric series", that it, a series where each term is some number r times the previous term



Variance Formula Calculation Examples With Excel Template



Http Hcgreen Weebly Com Uploads 4 4 3 1 Review Study Guide Series And Sequences Pdf
Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at Teachoo7 1 5 9 13 (4n 3) = 2n2 n Proof For n = 1, the statement reduces to 1 = 2 12 1 and is obviously true Assuming the statement is true for n = k 1 5 9 13 (4k 3) = 2k2 k;1/21/54/51 2/3 The calculator performs basic and advanced operations with fractions, expressions with fractions combined with integers, decimals, and mixed numbers It also shows detailed stepbystep information about the fraction calculation procedure Solve problems with two, three, or more fractions and numbers in one expression



Quartile Deviation Formula Calculator Examples With Excel Template




Solved P1 3 A Solve In Terms Of Geometric Series To Find Chegg Com
Transcript Prove 1 2 3 n = (n(n1))/2 for n, n is a natural number Step 1 Let P(n) (the given statement)\ Let P(n) 1 2 3 n = (n(n1))/2 Step We can also prove the given result using Mathematical Induction Let Sn = 123 234 345 n(n 1)(n 2) = n ∑ r=1r(r 1)(r 2) We want to prove that Sn = 1 4 n(n 1)(n 2)(n 3) ∀n ∈ N Let use consider the case n = 1 When n = 1 the given result givesWe need to give this a name so let f (n) = 1/ (1x2)1/ (2x3)1/ (3x4)1/ (n (n1)) The first thing we notice is that for n > 1, we are just adding another fraction to the previous value of f (n) So we can construct f (n) = f (n1) 1/ (n (n1)) Now look at the small values of n



Solved Situation Given Answer Standard Error Formula 1 Consider A Population Consisting Of N 1 2 3 4 5 8 9 And 11 Samples Of Size 3 Are D Course Hero
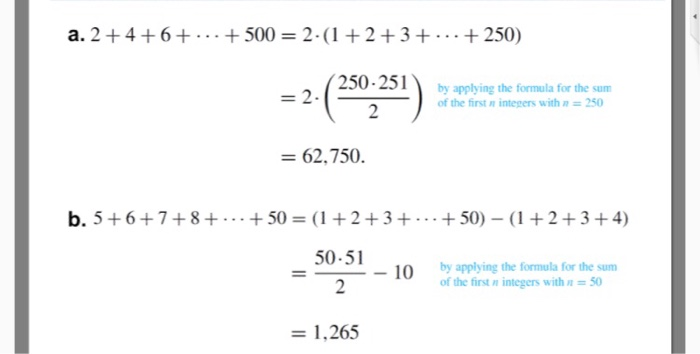



Solved B Multiply 5 Choose Sub 1 2 3 4 Q
For an AP, the sum of the first n terms can be calculated if the first term and the total terms are known The formula for the arithmetic progression sum is explained below Consider an AP consisting "n" terms S = n/2 2a (n − 1) × d This is the AP sum formula to find the sum of n terms in series Proof Consider an AP consistingTo find the Population Standard deviation of 1,2,3,4,5 Perform the steps 1 and 2 as seen in above example Step 3 Now find the population standard deviation using the formula √10/√5 = 1414 Variance Example To find the Variance of 1,2,3,4,5 After(13) we will prove that the statement must be true for n = k 1 1 5 9 13 4(k 1) 3 = 2(k 1)2 (k 1
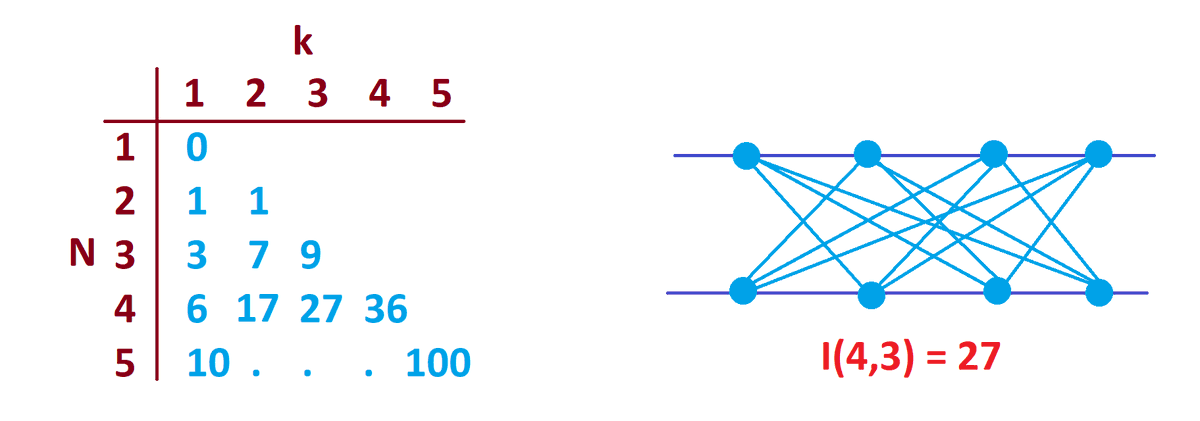



James Tanton Let I N K Max Possible Count Of Intersections That Can Occur If N Points On Each Of Two Parallel Lines Are Each Connected Via Line Segments To Precisely K
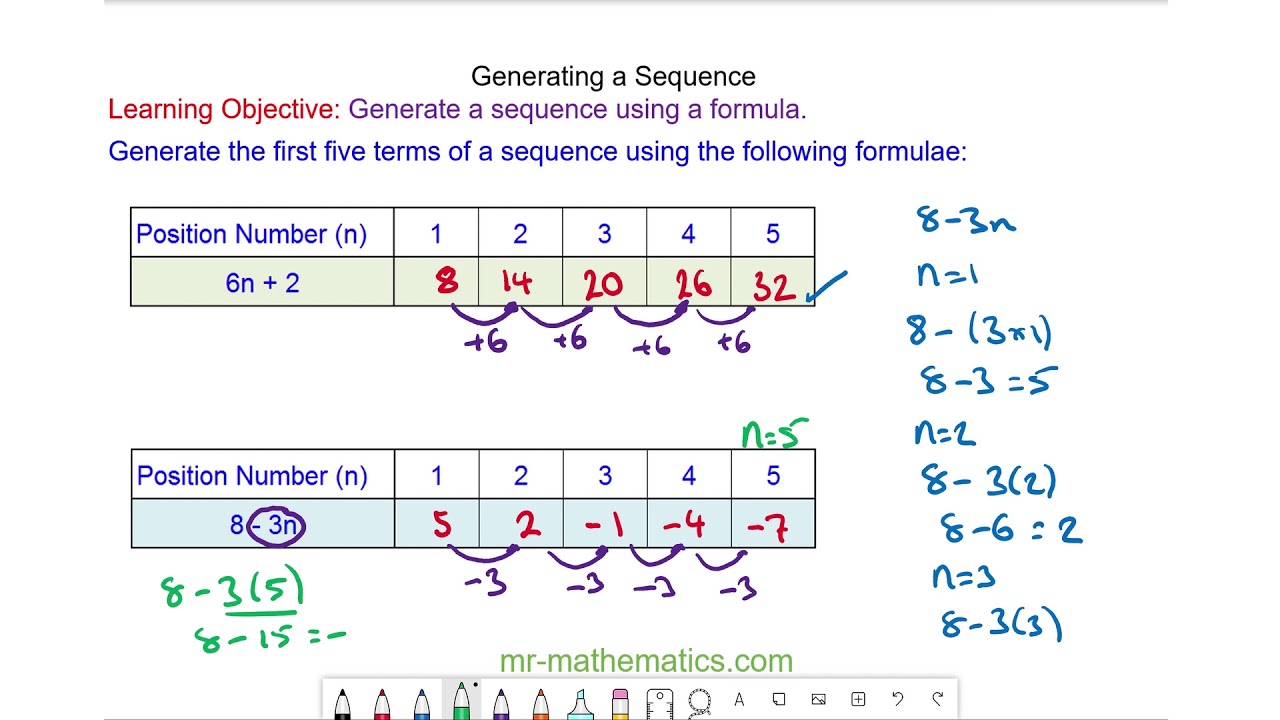



Generating Sequences From The Nth Term Youtube
This is one of those questions that have dozens of proofs because of their utility and instructional use I present my two favorite proofs one because of its simplicity, and one because I came up with it on my own (that is, before seeing others do it it's known) 1 3 5 7 (2k − 1) (2k 1) = k2 (2k 1) (from 1 by assumption) = (k 1)2 =RHS Therefore, true for n = k 1 Step 4 By proof of mathematical induction, this statement is true for all integers greater than or equal to 1 (here, it actually depends on what your school tells you because different schools have different ways What a big sum!



How To Get The Sum Of 1 2 3 4 5 6 N In C Language Using A Function Quora




Problem 3 A Find A Formula For 1 2 2 33 4 N N 1 We Chegg Com
(1) ethane (3) ethyne (2) ethene (4) ethanol 71 If a hydrocarbon molecule contains a triple bond, itsThis might take a while but stay with me Following idea is mentioned in the book Art of Problem Solving Let's start by calculating math \displaystyle\sum_{k=1}^{n} k^{2}/math and to do that we are going to take a combinatorial way Count theIn a way they all are, except multiple digit numbers (13, 21, etc) overlap , like this 00




Calculus 2 Infinite Sequences And Series 13 Of 62 Sequences Find The Formula Ex 3 Youtube
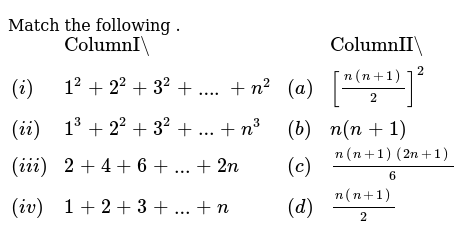



Mathod Of Induction 1 2 2 2 3 2 N 2 N N 1 2n 1 6
Find 3(3bromophenyl)4H1,2,4triazol5amine and related products for scientific research at MilliporeSigma I have come up with my own formula just comment if it is not correct to solve this series 1–23–45–649–50 Solution let n (subscript) be the number of terms in the series let S be the summation so, let solve first less series like, Sn = 1–To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=1234
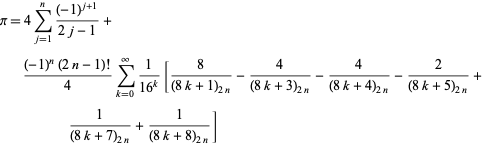



Pi Formulas From Wolfram Mathworld



Untitled Document
2 1 3 3 4 6 5 10 6 15 7 21 8 28 9 36 10 45 25 300 The total number of handshakes would be 300 Connecting Geometry to Advanced Placement Mathematics A Resource and Strategy Guide which was represented by n – 1 Thus the formula was 2 ( )( −1) = n n Total number of handshakes



Solved 5 11 17 23 29 Find The Thousandth Term A1000 Use Summation Notation To Write The Sum Of The First Thousand Terms Use The Sum Of Ari Course Hero




Answered 2 Find The Formula Of The General N Th Bartleby
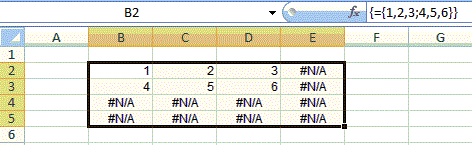



Excel Formula Arrays Repeating Value When Single Value Returned Microsoft Community



What Is The Explicit Formula For The Arithmetic Sequence In The Table Below N 1 2 3 4 5 An 9 2 7 4 Brainly Com



What Is The Formula For Summation Of 1 2 3 N




1 2 2 3 3 4 N N 1 Formula Novocom Top




What Is The Sum Of The Series 1 2 2 3 3 4 4 5 N N 1 Quora




Factorial Calculator Solve N Inch Calculator




Algebra Ii Chapter 11 Series Multiple Choice Identify The Choice That




Perfect Number Wikipedia
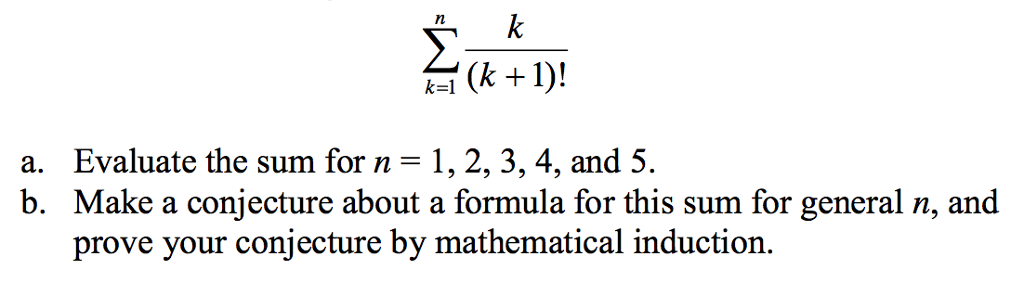



K 1 Evaluate The Sum For N 1 2 3 4 And 5 Make A Chegg Com



2




Answered I Proving A Formula Use Mathematical Bartleby




Proof Using Induction Payment Proof




Recursive Formula Explained W 25 Step By Step Examples
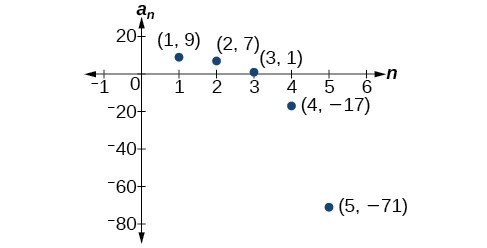



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




Please Help Asap Instructions Drag The Tiles To The Correct Boxes To Complete The Pairs Not All Tiles Brainly In



Fchsmrshaley Weebly Com Uploads 1 7 6 5 Sequences And Series Review Solutions Pdf




3 Find A Formula For The Sum Of 1 2 3 4 5 Gauthmath



3



How To Calculate 1 2 3 4 5 6 7 8 9 10 Quickly Quora




Answered Matching 1 Geometric Sequence 2 Bartleby
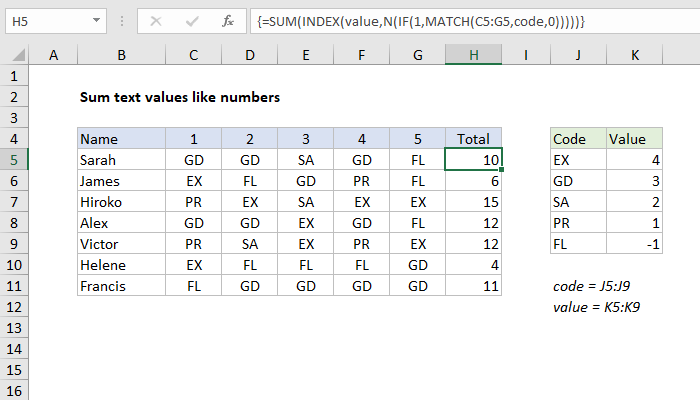



Excel Formula Sum Text Values Like Numbers Exceljet




Grade 10 Math Module 1 Searching For Patterns Sequence And Series




Standard Deviation For 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 21 22 23 24 And 25 Workout
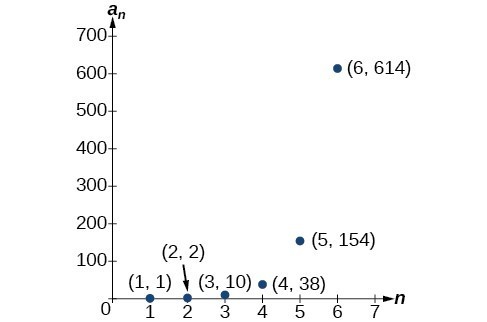



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




Chapter 5 Sets And Counting Goldsteinschniederlay Finite Math



Iopscience Iop Org Article 10 10 1742 6596 1008 1 0172 Pdf




Sequences As Functions Explicit Form Mathbitsnotebook A1 Ccss Math




Math 6 Section 700 Experimentation Conjecture And Reasoning Spring 05
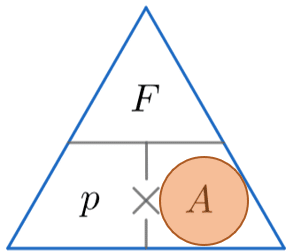



Pressure Force Area Questions Worksheets And Revision Mme




1 2 3 4 Wikipedia



Determine Whether The Points Are Collinear I A 1 3 B 2 5 C 4 7 Ii L 2 3 M 1 3 N 5 4 Sarthaks Econnect Largest Online Education Community



4 1 Higher Order Derivatives




n Formula
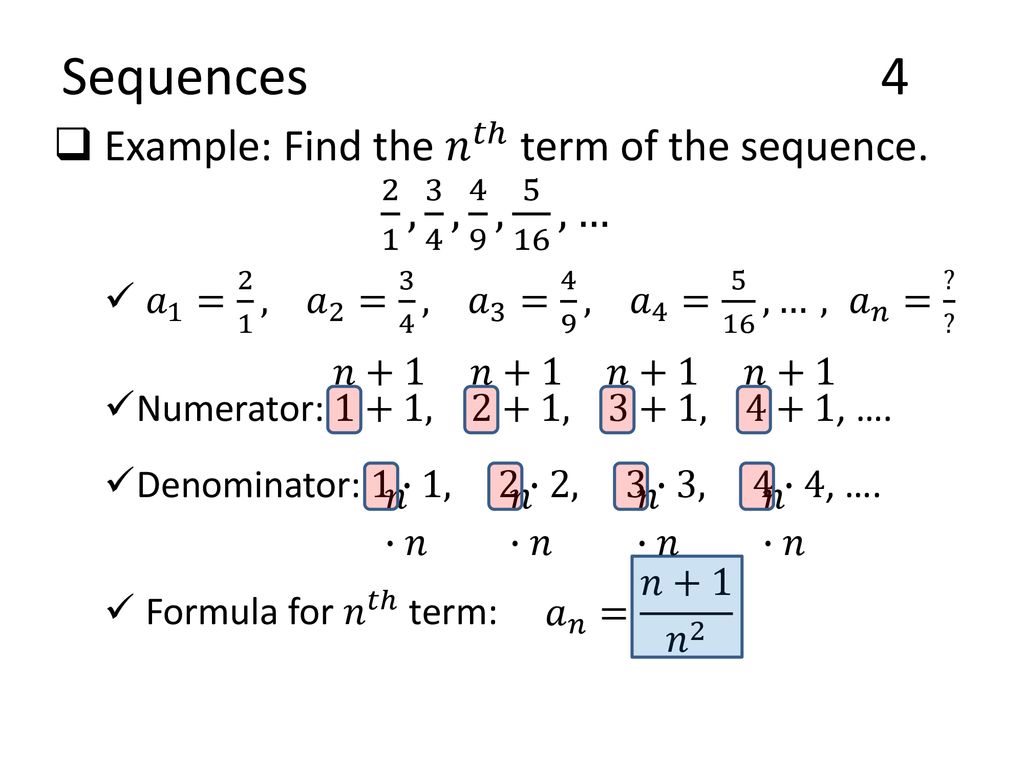



Sequences The Binomial Theorem Chapter Ppt Download




2 In This Question We Will Consider The Sum Of Chegg Com




1 2 3 4 Wikipedia




1234n Formula




A 29 Sequences




Prove By Mathematical Induction 3 4 5 N 2 N N Homeworklib




Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy




Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange




Situation Given Answer Error Formula 1 Conside Gauthmath




Find The Sum 4 5 1000 Using The Formula 1 2 3 N N 1 N 2 Youtube




Formulas To Sum The Lowest N Values From A Range In Excel



Quartile Formula How To Calculate Quartile In Statistics Example



Ben Collins Array Formulas Are Powerful Work With Ranges Of Data In Googlesheets Formulas Pressing Ctrl Shift Enter Pc Chromebook Or Cmd Shift Enter On A Mac



How To Calculate 1 2 3 4 5 6 7 8 9 10 Quickly Quora



Mynpc Npc Edu Ics Icsfs Math 105 Chapter One 2 Of 5 Pdf Target E03f64af 94e1 40 994e Cd218c6bfff8




Proof Of 1 2 2 2 Cdots N 2 N 3 3 N 2 2 N 6 Mathematics Stack Exchange
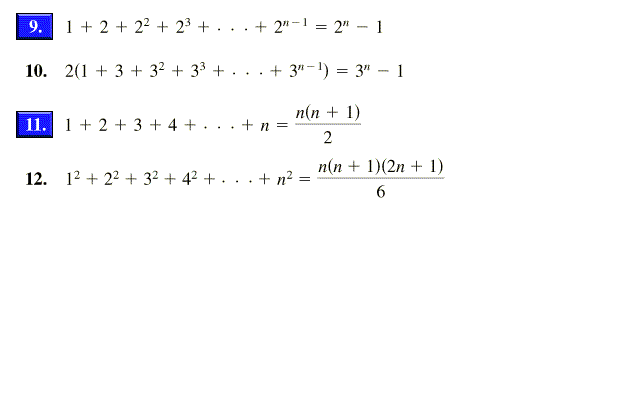



In Exercises 5 18 Use Mathematical Induction To Chegg Com



2



1



Combinations Calculator Ncr



Python Challenges 1 Exercises Practice Solution W3resource




In Exercises 5 18 Use Mathematical Induction To Chegg Com



Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Hw 85 key 9h Pdf



Let Function Xl N Cad
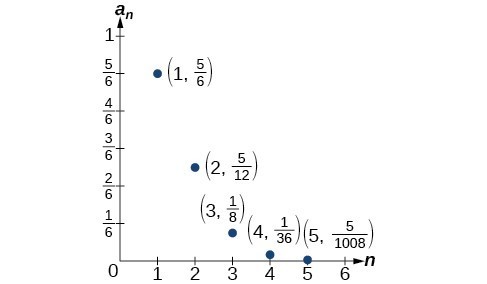



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




Sequences Arithmetic Sequences Examples




Copyright C Cengage Learning All Rights Reserved Ppt Download




Ethiopia Learning Math Grade 12 Page 15 In English




15 Average Formulas With Discussion In Hindi Youtube




The Nth Term Un Example If We Are Given A Formula For Un Th Nth Term Where Find The First Five Terms Of The Sequence Un 3n Ppt Download



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot



2




Average Formula Concepts Rules Practice Questions With Solutions




What Are Natural Numbers Definition Examples And Facts




Intro Math Problem Solving September 21 Factorials Stepping



1




Mathematical Induction And Binomial Theorem Summation Elementary Mathematics




4 What Formula Is Needed To 2 Points Get The Sequ Gauthmath




Find A Formula For The General Term A N Not The Chegg Com




8 41 If A 1 2 3 4 5 Then The Number Of Prop Gauthmath




5 4 Mathematical Induction T



0 件のコメント:
コメントを投稿